Teorema de Tales
Teorema de Tales afirma que um feixe de retas paralelas determina, em duas transversais quaisquer, segmentos proporcionais. Desse modo, se temos duas retas paralelas “cortadas” por duas transversais, os segmentos formados por essa intersecção são proporcionais.
Leia também: Duas retas paralelas cortadas por um transversal
Representação e fórmula
Para melhor entendermos o enunciado do teorema, representaremos graficamente o feixe de retas paralelas interceptadas por retas transversais.
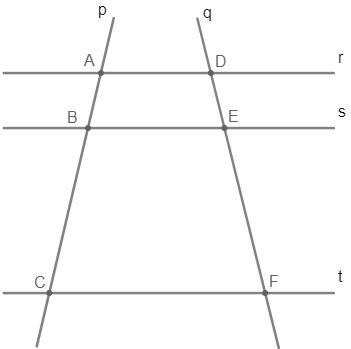
Observe que as retas r, s e t são paralelas e denotadas por r//s//t, as retas p e q são as transversais, os segmentos AB, BC, DE e EF foram determinados pelas intersecções das retas, e que, pelo teorema de Tales, esses segmentos são proporcionais, ou seja, as razões entre eles são iguais.
![]()
Em consequência das propriedades das proporções, podemos escrever o resultado do teorema de Tales destas maneiras:
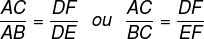
-
Exemplos
Na figura a seguir, r//s//t, determine as medidas dos segmentos.
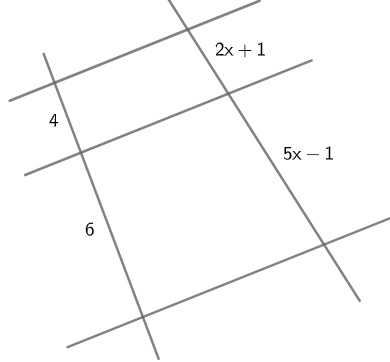
Aplicando o teorema de Tales, temos:
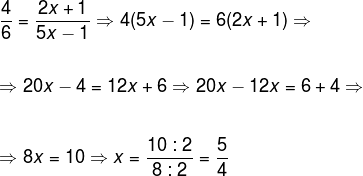
Para determinar a medida dos segmentos, devemos substituir os valores de x.
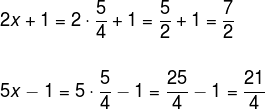

Teorema de Tales nos triângulos
O teorema de Tales aplicado nos triângulos é mais conhecido por teorema da bissetriz interna. Esse afirma que:
“Em todo triângulo, a bissetriz de qualquer ângulo interno divide o lado oposto a ele em duas partes proporcionais, em relação a seus lados adjacentes.”
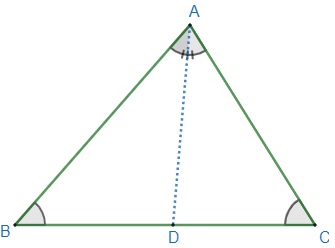
Observe que o segmento AD é a bissetriz do triângulo ABC, visto que ele divide o ângulo BÂC em duas partes iguais. De acordo com o teorema, o segmento de reta AD divide o lado oposto, ou seja, o lado BC, em dois segmentos proporcionais aos lados adjacentes, isto é, os lados AB e AC são proporcionais aos lados BD e DC nessa ordem, e, portanto, podemos escrever:
![]()
-
Exemplo
Considere o triângulo seguinte e determine o valor de x, sabendo que o segmento AD é a bissetriz relativa ao lado BC.
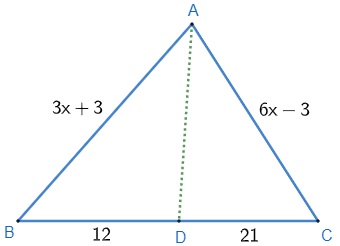
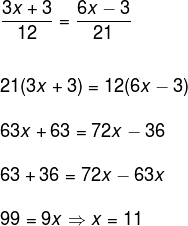
Saiba mais: Intersecção de retas concorrentes
Exercícios resolvidos
Questão 1 – (Enem) A planta de determinado bairro de uma cidade apresentou o desenho a seguir. O responsável pelo departamento de obras do município constatou a ausência de algumas medidas nessa planta, as quais ele representou no projeto por x e y.
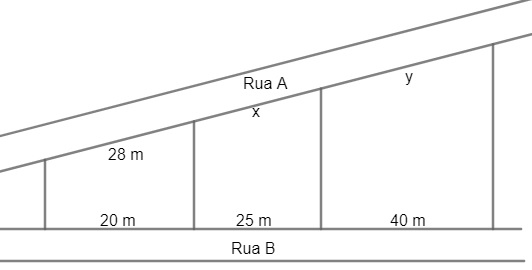
Com base nos dados do projeto, esse responsável pôde calcular corretamente os respectivos valores de x e y:
a) 35 m e 56 m
b) 25 m e 40 m
c) 35 m e 70 m
d) 56 m e 70 m
e) 56 m e 84 m
Solução
Observando a imagem, temos que o teorema de Tales pode ser aplicado na planta do bairro. Os segmentos que ligam as ruas A e B são paralelos, logo, temos:
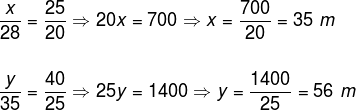
Portanto, os valores de x e y são, respectivamente, 35 m e 56 m.
R: alternativa a
Questão 2 – Em um triângulo ABC, o perímetro é 54 cm, BS é a bissetriz, AS = 8 cm, e SC = 10 cm. Determine a medida do lado AB.
Solução
Inicialmente vamos ilustrar o triângulo descrito no problema, nomeando x e y os lados dos quais não conhecemos a medida.
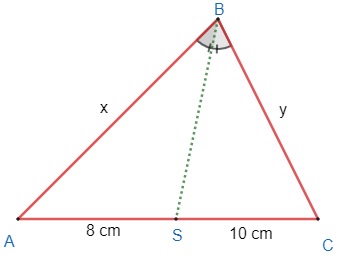
Como foi dado que o perímetro do triângulo ABC é 54 cm, temos que a soma de todos os lados é igual a 54 cm.
x + y + 18 = 54
x + y = 54 -18
x + y = 36
Por outro lado, podemos aplicar o teorema da bissetriz interna no triângulo ABC, tendo que:
![]()
Isolando o valor de x na primeira equação, temos que x = 36 – y, e substituindo esse valor na segunda equação, temos que:
10x = 8y
10 · (36 – y) = 8y
360 – 10y = 8y
360 = 8y + 10y
18y = 360
y = 20
Substituindo o valor de y em qualquer uma das equações, temos:
x = 36 – y
x = 36 – 20
x = 16
Portanto, o lado AB mede 16 cm.
Artigos Relacionados

Últimas notícias
Outras matérias


















