Obtendo uma reta tangente conhecendo um ponto e a circunferência
Existem três possibilidades para a posição relativa de um ponto em relação a uma circunferência. Partindo da análise desta posição, podemos encontrar a equação da reta que tangencia uma determinada circunferência, que contém este ponto analisado. Este estudo quanto à posição relativa dos pontos em relação à circunferência pode ser visto no artigo Posições Relativas De Duas Retas.
Sendo assim, comentaremos sobre cada posição relativa e sua respectiva consequência em relação à reta tangente.
Seja P o ponto que iremos analisar:
• P interno à circunferência, implica dizer que não é possível esboçar uma reta tangente.
• P sendo um ponto da circunferência. Neste caso o ponto P é o ponto de tangência e com isso será possível esboçar apenas uma reta tangente.
• P externo à circunferência. Podemos esboçar duas retas tangentes à circunferência que passam pelo ponto P.
Contudo, para sabermos qual a posição do ponto P em relação à circunferência, devemos calcular a distância do centro da circunferência até o ponto e compararmos ao raio da circunferência, leitura que pode ser vista no artigo citado acima.
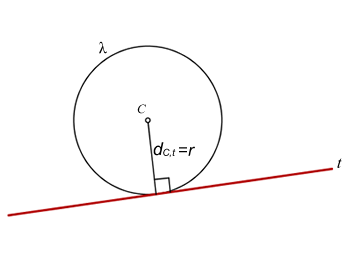
Para encontrarmos a equação da reta tangente, iremos utilizar a expressão da distância do centro da circunferência até a reta tangente, distância esta que deve ser igual a r.
Veremos então alguns exemplos que necessitam dessa análise e dos cálculos que devem ser realizados para encontrarmos a equação da reta tangente.
Determine as equações das retas tangentes à circunferência λ: x²+y²=1, traçadas pelo ponto P (√3, 0).
Primeiramente vamos verificar a posição relativa do ponto P em relação à circunferência.
C (0,0) e raio r=1. Com isso, calcularemos a distância do centro até o ponto P.
![]()
Sendo P um ponto externo, sabemos que por este ponto podemos traçar duas retas tangentes à circunferência. Neste momento vamos determinar a equação geral da reta tangente.
![]()
Para isso, precisamos partir das informações que temos a respeito desta reta, que é somente o ponto que ela passa P (3,0):
.png)
Note que precisamos determinar o valor do coeficiente angular (m) para obtermos a equação da reta tangente. Para isso, utilizaremos a expressão da distância do centro até a reta tangente:
.png)
Basta substituirmos na equação da reta tangente o valor de m, que iremos obter as duas retas tangentes:
.png)
Como vimos, encontramos duas equações de reta, que representam duas retas tangentes que passam pelo ponto P(√3,0) e tangenciam a circunferência λ: x2+y2=1.
Por Gabriel Alessandro de Oliveira
Graduado em Matemática
Artigos Relacionados

Últimas notícias
Outras matérias


















