Função raiz
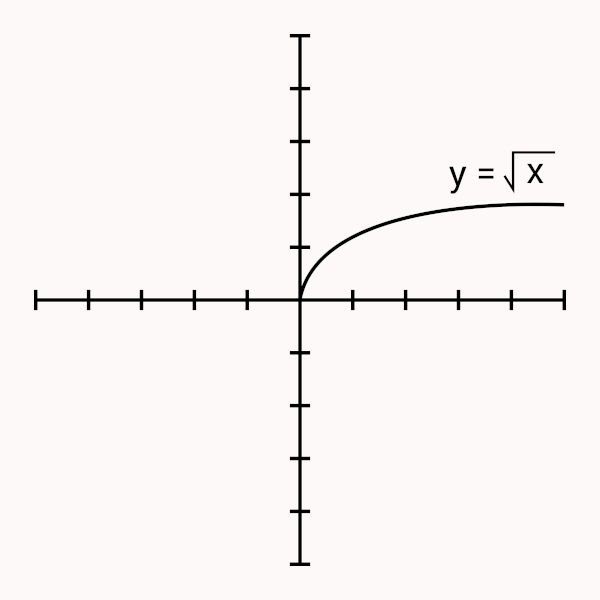
A função raiz é identificada quando na lei de formação da função a variável se encontra dentro de um radical. A função raiz quadrada e a função raiz cúbica são exemplos de função raiz. Como a maioria dos valores da imagem de uma raiz é um número irracional, a função raiz é considerada uma função irracional.
O conjunto do domínio da função possui restrição quando o índice da função for par, pois o radicando necessariamente tem que ser positivo para que exista raiz. No estudo das funções, é sempre possível realizar sua representação gráfica.
Veja também: Função polinomial — função em que a lei de formação pode ser descrita por um polinômio
Resumo sobre função raiz
-
A função raiz possui em sua lei de formação uma variável dentro do radical.
-
É preciso analisar o índice do radical da raiz para encontrar seu domínio.
-
Quando a função raiz possui índice par, o seu radicando é necessariamente positivo.
-
Não existe raiz com índice par de um número negativo no conjunto dos números reais.
-
A função raiz quadrada e a função raiz cúbica são exemplos de função raiz, sendo a primeira a mais comum.
Função raiz: o que é?
Quando uma função possui uma ou mais variáveis dentro de um radical, a chamamos de função raiz. Ela sempre terá uma raiz de índice n, sendo que a função raiz mais comum é a função raiz quadrada. Veja a lei de formação de algumas funções raiz a seguir:
➝ Lei de formação de algumas funções raiz
-
\(f\left(x\right)=\sqrt x\)
-
\(g\left(x\right)=\sqrt{x^2-2}\)
-
\(h\left(x\right)=1+\sqrt[3]{x-2}\)
-
\(i\left(x\right)=\sqrt[4]{\frac{x}{3}}\)
Como é o cálculo da função raiz?
Para calcular o valor numérico de uma função raiz, basta realizarmos a substituição da sua variável pelo valor desejado. Vale ressaltar que em muitos casos, o valor numérico de uma função raiz é um número irracional.
➝ Exemplos de cálculo da função raiz
- Exemplo 1:
Dada a função \(f\left(x\right)=\sqrt{x-4}\), calcule:
a) \(f\left(13\right)\)
b) \(f\left(7\right)\)
Resolução:
a) \(f\left(13\right)\)
Quando x = 13, temos:
\(f\left(13\right)=\sqrt{13-4}=\sqrt9=3\)
b) \(f\left(7\right)\)
Quando x = 7, temos:
\(f\left(7\right)=\sqrt{7-4}=\sqrt3\)
Como a \(\sqrt3\) é um número irracional, podemos afirmar que \(f\left(7\right)=\sqrt3\). Caso seja necessário calcular a raiz quadrada, utilizamos uma aproximação para essa raiz, como 1,7.
- Exemplo 2:
Dada a função \(g\left(x\right)=\sqrt[3]{x}+2x\), calcule \(g\left(8\right)\).
Resolução:
\(g\left(8\right)=\sqrt[3]{8}+2\cdot8\)
\(g\left(8\right)=2+16\)
\(g\left(8\right)=18\)
Domínio de uma função raiz
No estudo de uma função raiz, conhecendo a sua lei de formação, é importante compreender que nem sempre o domínio de uma função é o conjunto dos números reais, pois existe uma restrição na radiciação quando o índice da função é par. Sabemos que não existe raiz com índice par de um número negativo no conjunto dos números reais.
- Exemplo:
Considere a função a seguir:
\(f\left(x\right)=\sqrt{3x+4}\)
Qual é o conjunto domínio dessa função quando a analisamos no conjunto dos números reais?
Resolução:
Para que exista imagem para um determinado valor de x, temos:
\(3x\ +\ 4\ \geq\ 0\ \)
\(3x\ \geq\ -\ 4\ \)
\(x\geq-\frac{4}{3}\)
Assim, o domínio dessa função é:
\({\ x\ \in\ \mathbb{R}\ |\ x\ \geq\ -\frac{4}{3}}\)
|
Quando o índice da função raiz é ímpar, o domínio da função não tem restrição, podendo ser o conjunto dos números reais. |
Saiba também: Domínio, contradomínio e imagem de uma função — qual a diferença?
Gráfico da função raiz
O gráfico da função raiz é sempre crescente.
- Exemplos:
Quando a função raiz possui um índice par, seu gráfico estará somente no 1º quadrante:
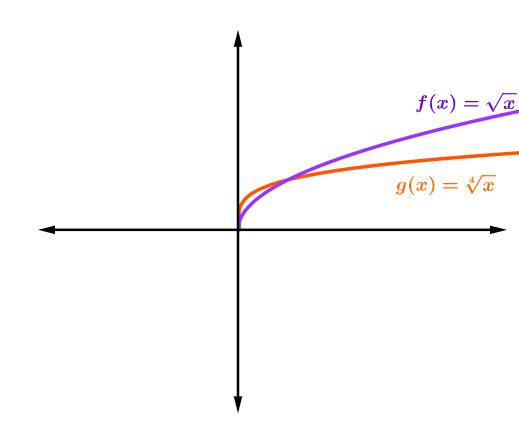
|
Perceba que ao aumentar o valor do índice, a função continua crescente. |
Quando a função possui índice ímpar, o gráfico da função raiz estará tanto no 1º quanto no 3º quadrante.
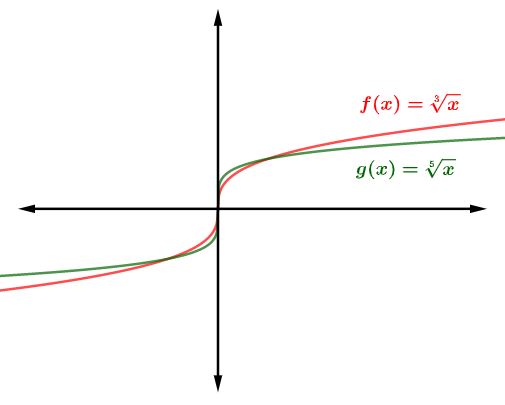
Leia também: Como é o gráfico de uma função exponencial?
Exercícios resolvidos sobre função raiz
Questão 1
Analisando a função \(\ f:\ A\ \rightarrow B\ \), com lei de formação \(f\left(x\right)=\sqrt[3]{x-4}\), julgue as afirmativas a seguir:
I) O domínio dessa função é necessariamente os valores de x, tal que \(x\geq\ 4\).
II) \(f\left(-4\right)=-2\)
III) Essa função é uma função raiz.
Marque a alternativa correta:
A) Somente a afirmativa I é falsa.
B) Somente a afirmativa II é falsa.
C) Somente a afirmativa III é falsa.
D) Todas as afirmativas são verdadeiras.
Resolução:
Alternativa A
I) Falsa
Como o índice da raiz é igual a 3, um número ímpar, o domínio dessa função pode ser o conjunto dos números reais, não havendo uma restrição para o valor de x.
II) Verdadeira
Calculando \(f\left(-4\right)\), temos:
\(f\left(-4\right)=\sqrt[3]{-4-4}\)
\(f\left(-4\right)=\sqrt[3]{-8}\)
\(f\left(-4\right)=-2\)
III) Verdadeira
Como a variável está dentro do radical, essa função é de fato uma função raiz.
Questão 2
Analisando a função \(f\left(x\right)=\sqrt{2x+6}\) no conjunto dos números reais, podemos afirmar que:
A) \(D\ =\ {x\ \in\ \mathbb{R}\ |\ x\ \geq\ 2}\)
B) \(D\ =\ {x\ \in\ \mathbb{R}\ |\ x\ \geq\ -6}\)
C) \(D\ =\ {x\ \in\ \mathbb{R}\ |\ x\ \geq\ -3}\)
D) \(D\ =\ {x\ \in\ \mathbb{R}\ |\ x\ \geq\ 4}\)
Resolução:
Alternativa C
Analisando a lei de formação, temos:
\(2x\ +\ 6\ \geq\ 0\)
\(2x\ \geq\ -6\)
\(x\geq\frac{-6}{2}\)
\(x\ \geq\ -3\ \)
Portanto:
\(D\ =\ x\ \in\ R\ |\ x\ \geq\ -3\)
Artigos Relacionados

Últimas notícias
Outras matérias


















