Equação reduzida da circunferência

A equação reduzida da circunferência é utilizada para representar de forma algébrica o comportamento da circunferência no plano cartesiano. A circunferência é o conjunto de pontos que estão a uma mesma distância do seu centro. A equação reduzida da circunferência é estudada na geometria analítica, que busca representar, de forma algébrica, os objetos geométricos.
Para encontrar a equação reduzida de uma circunferência qualquer, é necessário que a medida do raio e as coordenadas do centro da circunferência sejam conhecidas, pois a fórmula da equação reduzida da circunferência é (x – a)² + (y – b)² = r², em que (a, b) é a coordenada do centro da circunferência e r é o comprimento do seu raio.
Leia também: Equação reduzida da reta — a maneira de representar a reta de forma algébrica
Qual é a fórmula da equação reduzida da circunferência?
Sabemos que a circunferência é formada pelo conjunto de pontos que estão a uma mesma distância de determinado ponto. Essa distância fixa é conhecida como raio, e o ponto é conhecido como centro da circunferência. Quando representamos a circunferência no plano cartesiano, determinamos as coordenadas do seu centro C(a, b) e também o comprimento do seu raio.
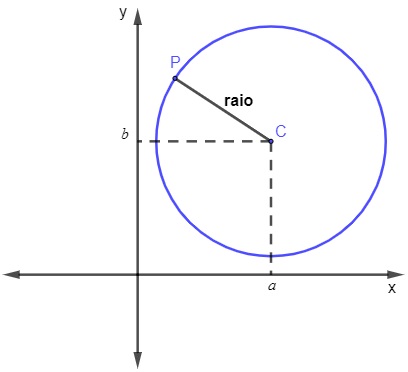
Por definição, sabemos que os pontos da circunferência estão a uma mesa distância do centro C, e que essa distância é igual ao raio r. Então temos que:
dPC = r
Entretanto, as coordenadas do ponto C são (a, b) e o ponto P é um ponto da circunferência qualquer com coordenadas (x, y). Utilizando a fórmula de distância entre dois pontos, temos que:
\(\left(x-a\right)^2+\left(y-b\right)^2=dPC²\)
A distância entre os dois pontos é igual ao raio, então é possível deduzir a equação reduzida da circunferência, que é:
\(\left(x-a\right)^2+\left(y-b\right)^2=r²\)
Como determinar a equação reduzida da circunferência?
Para determinar a equação reduzida da circunferência, basta substituir na fórmula da equação reduzida da circunferência os valores encontrados para as coordenadas do centro e o valor do raio. Então precisamos dos valores de C(a, b) e r.
Exemplo:
Determine a equação reduzida da circunferência de centro C(1, 2) e raio r = 8.
Resolução:
Temos que a = 1, b = 2 e r = 8. Substituindo na equação, temos que:
\(\left(x-a\right)^2+\left(y-b\right)^2=r^2\)
\(\left(x-1\right)^2+\left(y-2\right)^2=8^2\)
Resolvendo a potência de 8², encontraremos a equação reduzida da circunferência:
\(\left(x-1\right)^2+\left(y-2\right)^2=64\)
Exemplo 2:
Determine a equação reduzida da circunferência representada no plano cartesiano:
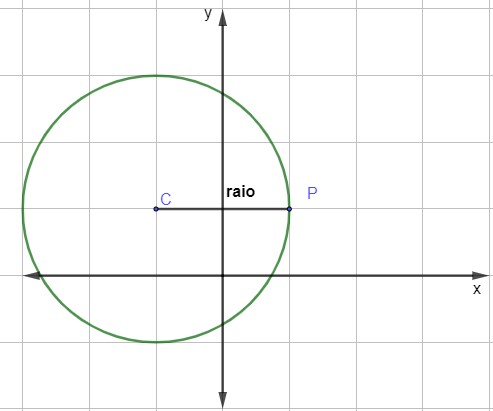
Resolução:
Sabemos que a coordenada do ponto C é (-1, 1), e, analisando a distância do ponto C ao ponto P, temos duas unidades, ou seja, r = 2. Então a equação reduzida dessa circunferência é:
\(\left(x-\left(-1\right)\right)^2+\left(y-1\right)^2=2^2\)
\(\left(x+1\right)^2+\left(y-1\right)^2=4\)
Importante: Podemos também encontrar o centro e o raio da circunferência por meio da sua equação, como nos exemplos a seguir:
(x – 2)² + (y – 1)² = 9
Essa é a equação reduzida da circunferência de centro C(2, 1).
Sabemos também que r² = 9, então \(r=\sqrt9\), logo, o raio da circunferência é r = 3.
(x + 1)² + (y – 4)² = 144
Essa é a equação reduzida da circunferência de centro C(-1, 4).
Temos que r² = 144, então o raio é \(r=\sqrt{144}\), logo, r = 12.
x² + y² = 16
Essa é a equação reduzida da circunferência de centro C(0, 0).
Temos r² = 16, então \(r=\sqrt{16}\), logo, r = 4.
Exercícios resolvidos sobre equação reduzida da circunferência
Questão 1
Uma circunferência tem raio medindo 10 e centro C(0, 2). Nessas condições, podemos afirmar que a equação reduzida dessa circunferência é:
A) (x – 2)² + (y – 2)² = 10
B) x² + y² = 10
C) x² + (y – 2)² = 100
D) (x – 2)² + y² = 100
E) x² + 2y² = 100
Resolução:
Alternativa C
Substituindo o valor do raio e do centro na equação da circunferência, temos que:
\(\left(x-a\right)^2+\left(y-b\right)^2=r^2\)
a = 0, b = 2 e r = 10
\(\left(x-0\right)^2+\left(y-2\right)^2={10}^2\)
Então a equação reduzida dessa circunferência é:
\(x^2+\left(y-2\right)^2=100\)
Questão 2
(Enem) A figura mostra uma criança brincando em um balanço no parque. A corda que prende o assento do balanço ao topo do suporte mede 2 metros. A criança toma cuidado para não sofrer um acidente, então se balança de modo que a corda não chegue a alcançar a posição horizontal.
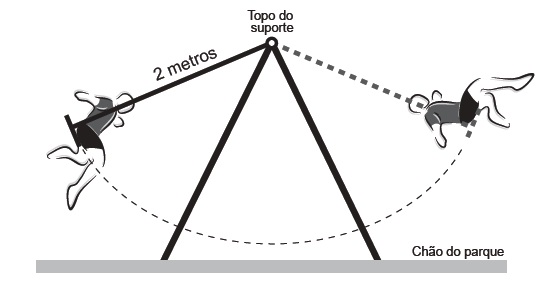
A curva determinada pela trajetória do assento do balanço é parte do gráfico da função:
A) \( f\left(x\right)=-\sqrt{2-x}\)
B) \( f\left(x\right)=\sqrt{2-x^2}\)
C) \( f\left(x\right)=x^2-2\)
D) \( f\left(x\right)=-\sqrt{4-x^2}\)
E) \( f\left(x\right)=\sqrt{4-x^2}\)
Resolução:
Alternativa D
Sabemos que o centro dessa circunferência é o ponto C(0, 0), que é o centro do suporte, além disso, que o seu raio é igual a 2, então sua equação seria:
\(\left(x-0\right)^2+\left(y-0\right)^2=2^2\)
\(x^2+y^2=4\)
Seja y = f(x), vamos isolar essa variável:
\(f\left(x\right)^2=4-x^2\)
\(f\left(x\right)=\pm\sqrt{4-x^2}\)
Note que a curva descreve só a parte de baixo da circunferência, que é a parte negativa, então temos que:
\(f\left(x\right)=-\sqrt{4-x^2}\)
Artigos Relacionados

Últimas notícias
Outras matérias


















