Conjuntos
Um conjunto é estabelecido quando agrupamos elementos com as mesmas características. Esses agrupamentos possuem notação própria, utilizando-se letras maiúsculas para dar nome a eles, e representação específica, em geral por meio de círculos, formando-se o que se conhece como diagrama de Venn, ou listando-se os elementos dos conjuntos.
Leia também: Teoria dos conjuntos: o que estuda e para que serve?
Notação e representação de um conjunto
Quando estudamos conjunto, devemos inicialmente compreender o modo como representamos e denotamos alguns elementos. Em geral, utiliza-se letras maiúsculas para nomear um conjunto.
Podemos representar um mesmo conjunto de diferentes modos. Veja:
- Exemplo
Representação do conjunto dos números pares menores que 10.
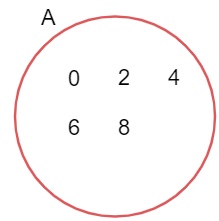
Os elementos do conjunto A são os números pares menores que 10. Na representação gráfica, os elementos devem ficar no interior do círculo, essa representação é conhecida por diagrama de Venn-Euler. Podemos representar também o conjunto fazendo uma lista de seus elementos:
A = {0, 2, 4, 6, 8}
Ao representarmos um conjunto na forma de lista, devemos separar os elementos por vírgula ou ponto e vírgula. Podemos representar o conjunto dos pares menores que 10 também assim:
A = { p | p é par menor que 10}
O qual lemos da seguinte forma: “p tal que p é par menor que 10”.
Relação de pertinência
A relação de pertinência mostra se um elemento está dentro ou não de um conjunto, ou seja, se ele pertence ou não pertence a um conjunto. Vamos utilizar os seguintes símbolos para a relação de pertinência.

Assim, para afirmar se um elemento está ou não no conjunto, devemos utilizar a notação anterior. Veja:
- Exemplo
Considere o conjunto B = {1, 3, 5, 7, 9, 11, 15}.
Observe que o elemento 5 está dentro do conjunto B e que o elemento 0, por exemplo, não está, assim:
![]()
Relação de inclusão
A relação de inclusão mostra-nos se um conjunto está contido ou não dentro de outro. Na relação de inclusão, utilizamos os seguintes símbolos:

- Exemplo
Considere os conjuntos:
A = {1, 2, 3, 4, 5}
B = {2, 3}
C = {5, 6, 7}
Observe que o conjunto B está por completo dentro do conjunto A, portanto, o conjunto B está contido no conjunto A.
A ⸦ B
Por outro lado, o conjunto C não está por completo no conjunto A, logo, o conjunto C não está contido no conjunto A.
![]()
Para que o conjunto A esteja contido no conjunto B, todos os elementos de A devem estar no conjunto B.
Veja mais: Conjuntos e seus elementos: relações e representações
Subconjuntos
A ideia de subconjunto está ligada à relação de inclusão, dizemos que A é subconjunto de B se, e somente se, todos os elementos de A forem elementos de B, ou seja, se A⸦ B, então A é subconjunto de B.
- Exemplo
Considere os conjuntos A = {a, b, c, d, e} e B ={a, b, c, d, e, f, g, h}.
Observe que todos os elementos de A são elementos de B, portanto, A é subconjunto de B, isto é: A ⸦ B.
O contrário já não é verdade, pois nem todo elemento de B é elemento de A, portanto, B não é subconjunto de A.
Conjunto unitário
Um conjunto é dito unitário se ele possuir um único elemento. Veja o exemplo:
- Exemplo
O conjunto A é unitário.
A = {7}
Conjunto universo
O conjunto universo é o que contém todos os outros conjuntos. Por exemplo, considere os conjuntos A = {– 1, – 2, 1, 2}, B ={0, 1, 2, 3} e C = {1, –1, 2, –2}, veja que todos eles são compostos por números inteiros, ou seja:
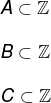
Portanto, o conjunto dos números inteiros é o conjunto universo.
Conjunto complementar
Considere dois conjuntos A e B de forma que A ⸦ B.
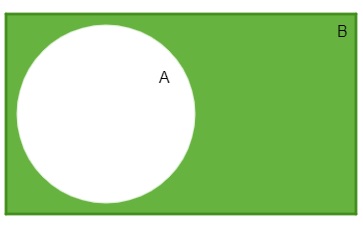
O conjunto complementar é formado pela diferença B – A, ou seja, tomamos os elementos de B e retiramos os elementos de A contidos em B. Esse conjunto é chamado complementar de B em relação a A.
Conjuntos das partes
O conjunto das partes de A é formado por todos os possíveis subconjuntos dos elementos do conjunto A. Veja o exemplo:
- Exemplo
Determine o conjunto das partes do conjunto A = {1, 2, 3}
O conjunto das partes é denotado por P (A) = {{1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}, {}}.
Para determinar o número de elementos do conjunto das partes de A, basta resolver a potência 2n, em que n é o número de elementos do conjunto A. Do exemplo 6, temos que o número de elementos de A é 3, logo, o número de elementos do conjunto das partes de A será:
23
2 · 2 · 2
8
Observação: O conjunto vazio {} está contido em todo conjunto.
Igualdade de conjuntos
Dois conjuntos serão iguais se, e somente se, apresentarem os mesmos elementos em qualquer que seja a ordem. Desse modo, os conjuntos a seguir são iguais:
A = {1, 2, 3, 4, 5, 6}
B = {6, 5, 4, 3, 2, 1}
C = {6, 6, 5, 4, 5, 4, 3, 6, 2, 1}
Note que os conjuntos A, B, e C possuem os mesmos elementos, ainda que no conjunto C exista repetições, a definição de Igualdade de conjunto leva em consideração somente a presença do elemento.
Acesse também: Noções importantes para o estudo da teoria dos conjuntos
Operações com conjuntos
-
União de conjuntos
Considere dois conjuntos A e B, a união entre eles será um novo conjunto formado por elementos de A ou elementos de B.
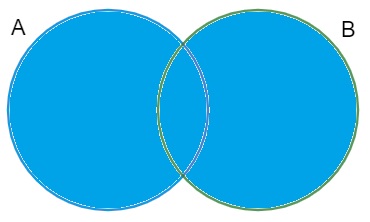
Representamos a união com o símbolo U, então A U B é a união entre os conjuntos A e B.
- Exemplo
Considere os conjuntos A = {a, b, c, d, e} e B ={c, d, e, f, g}.
Para determinar o conjunto união, basta escrever o conjunto formado por elementos que estão em ambos conjuntos, assim:
A U B = {a, b, c, d, e, f, g}
-
Intersecção de conjuntos
A interseção de conjuntos é formada por elementos que estão simultaneamente nos conjuntos envolvidos. Assim, considerando dois conjuntos A e B, a interseção é formada por elementos que pertencem ao conjunto A e ao conjunto B. Denotamos a interseção por ∩.
- Exemplo
Considere os conjuntos A = {a, b, c, d, e} e B ={c, d, e, f, g}.
Para determinar a intersecção entre os dois conjuntos, devemos encontrar os elementos que pertencem a eles.
A ∩ B = {c, d, e}
Exercícios resolvidos
Questão 1 – Considere os conjuntos A = {a, b, c, d, e, f} e B ={d, e, f, g, h, i}. Determine (A – B) U (B – A).
Resolução
Vamos determinar os conjuntos A – B e B – A e, em seguida, realizar a união entre eles.
A – B = {a, b, c, d, e, f} – {d, e, f, g, h, i}
A – B = {a, b, c}
B – A = {d, e, f, g, h, i} – {a, b, c, d, e, f}
B – A = {g, h, i}
Desse modo, (A – B) U (B – A) é:
{a, b, c} U {g, h, i}
{a, b, c, g, h, i}
Questão 2 – Determine o valor de x para que os conjuntos A = {1, 1, 2, 3} e B = {1, x, 3} sejam iguais.
Resolução
Vimos que dois conjuntos são iguais se todos os seus elementos forem iguais independentemente da ordem. Observando os conjuntos A e B, veja que o único elemento que falta no conjunto B para que A = B é o número 2, uma vez que elementos repetidos podem ser considerados como um só. Portanto:
x = 2
Questão 3 – Considere os conjuntos A = {a, b, c, d}, B= {c, d, e, f, g} e C = {b, d, e, g}. Determine os conjuntos:
a) B – A
b) A – C
c) A – B
Resolução
a) Para determinar o conjunto B – A, devemos considerar os elementos do conjunto B e retirar os elementos de A que pertencem ao conjunto B.
B – A = {e, f, g}
b) De maneira análoga, devemos considerar os elementos do conjunto A e retirar os elementos do conjunto C.
A – C = {a, c}
c) Da mesma maneira, determinamos o conjunto A – B.
A – B = {a, b}
Observe que A – B é diferente de B – A.
Artigos de Conjuntos

Últimas notícias
Outras matérias


















